統計の勉強をしていると、必ず登場するのが「σ(シグマ)」というギリシャ文字です。
見たことはあっても「どう読むの?」「何を意味しているの?」と迷った経験はありませんか。
この記事では、統計で使われる記号σ(シグマ)の読み方・意味・正しい書き方を、初心者にも分かるようにやさしく解説します。
また、数学でよく使われる大文字のΣ(シグマ)との違いや、2σ・3σといった品質管理での使われ方も紹介。
この記事を読めば、「σ=標準偏差」という関係がしっかり理解でき、データを見る目が確実にレベルアップします。
「ギリシャ文字は苦手」と感じる人こそ、まずはこのσから学び始めましょう。
標準偏差の記号「σ(シグマ)」とは?基本の意味をやさしく解説
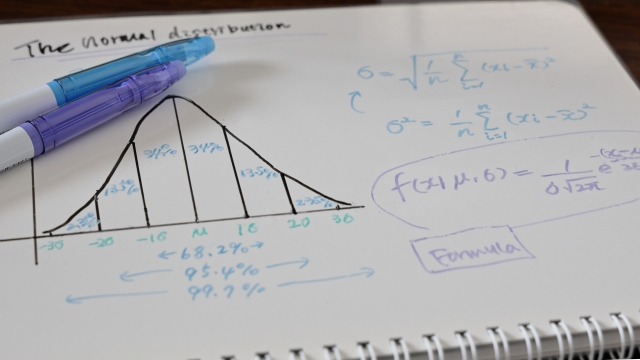
統計を学び始めると、必ず登場するのが「σ(シグマ)」というギリシャ文字です。
見た目は小文字のアルファベットのようですが、統計学ではとても重要な意味を持っています。
この章では、σが何を表しているのか、どんな場面で使われるのかを初心者にも分かるように解説していきます。
標準偏差とは何か?データのばらつきを表す指標
まず、「標準偏差」という言葉の意味から整理しましょう。
標準偏差とは、データのばらつき(散らばり具合)を数値で表したものです。
平均値が同じでも、個々のデータの広がり方が違えば、標準偏差の値も異なります。
つまり、標準偏差が小さいほどデータが平均値の近くに集まっており、大きいほどバラつきが大きいことを意味します。
| 例 | データ | 標準偏差の特徴 |
|---|---|---|
| パターンA | 50, 51, 49, 50 | ばらつきが小さい(標準偏差が小) |
| パターンB | 40, 60, 55, 45 | ばらつきが大きい(標準偏差が大) |
σ(シグマ)は、この「標準偏差」という概念を象徴する記号です。
σ(シグマ)の読み方とギリシャ文字の由来
σの読み方は「シグマ」です。
これはギリシャ文字のひとつで、英語のアルファベットでいえば「s」に相当します。
なぜ「s」に対応しているかというと、英語で標準偏差は「standard deviation」と呼ばれ、頭文字のsを表すためです。
そのため、標準偏差=σと覚えると理解しやすいでしょう。
| 記号 | 読み方 | 意味 |
|---|---|---|
| σ(小文字シグマ) | シグマ | 標準偏差を表す |
| Σ(大文字シグマ) | シグマ | 合計を表す |
同じ「シグマ」でも大文字と小文字でまったく意味が違うため、注意が必要です。
σが使われるシーン:統計・品質管理・心理学データなど
σは統計学以外にも、品質管理や心理学のデータ分析など、さまざまな分野で登場します。
たとえば、製品の品質のばらつきを管理する「シックスシグマ(6σ)」では、標準偏差の考え方を応用しています。
心理学では、テスト結果の分布を評価する際に標準偏差が使われます。
σは「データがどれだけ安定しているか」を測る共通言語なのです。
| 分野 | σの使われ方 |
|---|---|
| 統計学 | データのばらつきを測定 |
| 品質管理 | 製品の安定性や精度を評価 |
| 心理学 | テスト結果や傾向分析に利用 |
このように、σを理解することは、科学的な思考を身につける第一歩になります。
まずは「σ=標準偏差」という関係をしっかり頭に入れておきましょう。
σ(シグマ)の書き方と使い方を覚えよう
σ(シグマ)は、単に記号として知っているだけでは不十分です。
手書きで正しく書けるようにし、その意味や使われ方も理解しておくと、統計の基礎力がぐっと高まります。
この章では、σの正しい書き方や使われる文脈を、実際の場面に即して解説します。
σの正しい書き順と形のコツ
σの形は一見シンプルですが、正しく書くにはいくつかのポイントがあります。
まず、円を反時計回りに描き、その円の右上から少し外に向かって短い直線を引きます。
これがσの基本形です。
「丸を書いて右にチョン」と覚えると簡単です。
| ステップ | 動作 | ポイント |
|---|---|---|
| ① | 左上から反時計回りに円を描く | 円の中心が少し上にくるように意識する |
| ② | 右上に小さな直線を出す | 角度をつけすぎず、軽く添える程度でOK |
なお、フォントによっては印字されたσが少し異なる形をしていることもあります。
重要なのは「シグマ」と認識される形を崩さないことです。
手書きで書くときに注意すべきポイント
ノートや試験でσを書く際、意外と多いのが「数字の6」や「アルファベットのg」との書き間違いです。
この混同を防ぐには、σの「右上の突起」をしっかり書くことが大切です。
また、書き順を守ると自然と正しい形になります。
σは文字というより“記号”として書く意識を持つことがコツです。
| よくある間違い | 原因 | 修正ポイント |
|---|---|---|
| 数字の6のようになる | 突起が内側に入りすぎている | 突起を外側に伸ばす |
| gのように見える | 下部が長くなりすぎ | 円の高さを小さめに調整 |
また、プレゼン資料やレポートではフォント指定によりσが正しく表示されないこともあります。
その場合は、ギリシャ文字入力(Windowsなら「Alt+963」など)を使うと確実です。
2σ・3σとは?品質管理でよく出る「シグマ値」の意味
統計や品質管理の現場で、「2σ(ツーシグマ)」や「3σ(スリーシグマ)」という表現を見かけたことがあるかもしれません。
これは、平均値からのズレ(ばらつき)の範囲を表す尺度です。
データが正規分布している場合、平均値±1σの範囲には全体の約68%、±2σには約95%、±3σには約99.7%のデータが含まれます。
| 範囲 | 含まれる割合 | 意味 |
|---|---|---|
| ±1σ | 約68% | 大半のデータがこの範囲に収まる |
| ±2σ | 約95% | ほとんどのデータをカバーする |
| ±3σ | 約99.7% | ごくわずかな例外を除く全体 |
「シックスシグマ」という品質改善手法も、この3σの考え方を極限まで高めたものです。
つまり、標準偏差σはデータのばらつきを表すだけでなく、品質の安定性を測る指標としても活用されています。
数学で使うΣ(大文字シグマ)との違い
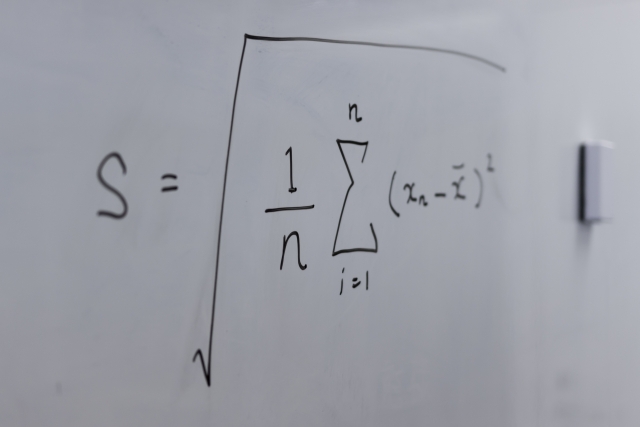
統計の世界で出てくる「σ(シグマ)」と、数学の式で見かける「Σ(シグマ)」は、見た目が似ています。
しかし、この2つはまったく別の意味を持っています。
この章では、両者の違いを整理しながら、混同しないための理解ポイントを紹介します。
Σ(シグマ)は「合計」を意味する記号
数学における大文字のΣ(シグマ)は、「合計する」という操作を表す記号です。
たとえば、1から5までの数字を足し合わせる場合、次のように表します。
Σ(i=1~5)i = 1+2+3+4+5
つまり、Σは「足し算の省略記号」のような役割を持っているのです。
| 記号 | 読み方 | 意味 |
|---|---|---|
| Σ(大文字シグマ) | シグマ | 合計(総和)を表す |
| σ(小文字シグマ) | シグマ | 標準偏差(ばらつき)を表す |
どちらも「シグマ」と読みますが、役割はまったく異なります。
Σは“足し算の操作”、σは“データのばらつき”を示すと覚えておくと混乱しにくいです。
小文字σとの使い分けを理解するコツ
同じ読み方をする2つの記号を区別するためには、「文脈」で判断するのがコツです。
統計学の話題やデータ解析の文脈ならσ(標準偏差)、数列や式の中に出てくるならΣ(合計)です。
つまり、σは“結果の広がり”を示し、Σは“計算の過程”を示す記号と考えると理解しやすいでしょう。
| 使用分野 | 記号 | 意味 |
|---|---|---|
| 統計学 | σ(小文字) | 標準偏差(データの散らばり) |
| 数学 | Σ(大文字) | 合計(総和) |
特にレポートや論文では、σとΣを誤記すると意味がまったく変わってしまうため注意が必要です。
例題で見るσとΣの違い
具体例で2つの違いを確認しましょう。
例1:数学のΣ
Σ(i=1~4)i² = 1²+2²+3²+4² = 30
これは単なる「合計」を表します。
例2:統計のσ
データが {2, 4, 4, 6, 8} の場合、平均値は4.8です。
それぞれのデータが平均からどれだけ離れているかを計算し、分散の平方根をとると標準偏差σが求まります。
| データ | 平均との差 | 差の2乗 |
|---|---|---|
| 2 | -2.8 | 7.84 |
| 4 | -0.8 | 0.64 |
| 4 | -0.8 | 0.64 |
| 6 | 1.2 | 1.44 |
| 8 | 3.2 | 10.24 |
分散=(7.84+0.64+0.64+1.44+10.24)÷5=4.16
標準偏差σ=√4.16=約2.04
このように、Σは計算の途中に使われ、σはその結果として表れる数値です。
“足すのがΣ、まとまりを見るのがσ”と区別して覚えましょう。
標準偏差σの計算と実例で理解する仕組み
ここまでで、σ(シグマ)の意味や読み方を理解できたと思います。
しかし、「実際にどうやって標準偏差を計算するのか?」という点でつまずく人も多いです。
この章では、具体的なデータを使いながら、標準偏差の計算方法をステップごとに見ていきましょう。
平均と分散、標準偏差の関係
標準偏差を理解するには、「平均」と「分散」という2つの考え方が欠かせません。
平均は「データの真ん中」を表し、分散は「その平均からどのくらいズレているか」を表します。
そして、標準偏差は分散の平方根をとった値です。
つまり、標準偏差=√分散 という関係が成り立ちます。
| 名称 | 意味 | 式 |
|---|---|---|
| 平均 | データの中心値 | (全データの合計)÷(データ数) |
| 分散 | データのばらつき | Σ(各データ−平均)² ÷ n |
| 標準偏差 | ばらつきの大きさ | √(分散) |
このように、標準偏差は分散を「平方根」で戻したものなので、単位も元のデータと同じになります。
たとえば、身長データなら分散の単位はcm²、標準偏差の単位はcmとなります。
エクセルや電卓での標準偏差の求め方
手計算で標準偏差を求めるのは手間がかかりますが、エクセルや関数電卓を使えば一瞬で計算できます。
エクセルでは、次のような関数を使います。
| 関数名 | 対象 | 説明 |
|---|---|---|
| =STDEV.P(範囲) | 母集団全体 | データ全体を1つの集団とみなす場合に使用 |
| =STDEV.S(範囲) | 標本 | 母集団の一部から計算する場合に使用 |
母集団と標本の違いを意識することが正確な分析の第一歩です。
関数を使えば、データ分析ツールが自動的にΣや平均などを処理してくれるため、計算ミスを防げます。
実際のデータを使ったσの読み解き方
次に、標準偏差の値を「どう読み解くか」を見てみましょう。
以下の表は、2つのクラスのテスト結果を比較したものです。
| クラス | 平均点 | 標準偏差(σ) | 特徴 |
|---|---|---|---|
| Aクラス | 70点 | 3 | 点数が平均付近に集中している |
| Bクラス | 70点 | 15 | 成績の差が大きく、バラつきがある |
平均点は同じでも、Aクラスは点数が揃っており、Bクラスは成績の差が大きいことがわかります。
このように、標準偏差を比較すると「どちらが安定しているか」「どれだけ偏りがあるか」が一目でわかります。
標準偏差は、単なる数値ではなく“データの性格”を映す鏡のような指標なのです。
また、標準偏差を使えば、異なる分野のデータでも「安定性」を比較できます。
たとえば、株価の変動(ボラティリティ)や品質管理の精度比較にも応用されます。
| 分野 | 例 | 標準偏差の意味 |
|---|---|---|
| 金融 | 株価の変動 | 値動きの激しさ |
| 教育 | 試験結果 | 生徒の理解度のばらつき |
| 製造 | 製品寸法の精度 | 品質の安定性 |
σの数値を“読む力”こそ、統計リテラシーの第一歩です。
まとめ|σ(シグマ)を理解すれば統計がもっと身近になる

ここまで、σ(シグマ)の意味・読み方・書き方、そして数学のΣとの違いを詳しく見てきました。
最後に、この記事のポイントを整理しながら、σを学ぶ意義をもう一度確認しておきましょう。
σの意味・読み方・書き方の要点整理
まずは、σに関する基本事項を振り返ります。
| 項目 | 内容 |
|---|---|
| 記号 | σ(ギリシャ文字の小文字) |
| 読み方 | シグマ |
| 意味 | 標準偏差(データのばらつきを表す) |
| 書き方 | 反時計回りに円を描き、右上に直線を加える |
σは「データの安定性」を示す重要な記号です。
σ=標準偏差という関係を覚えておくことが、統計学を理解する第一歩です。
標準偏差を使いこなすための次のステップ
標準偏差を理解できたら、次は「分布」と「確率」の考え方に進むとより深く統計を使いこなせます。
特に、正規分布や偏差値(deviation score)はσの考え方を基に成り立っています。
つまり、σを理解すれば、統計の世界の多くの概念がつながるのです。
| ステップ | 次に学ぶ内容 | 目的 |
|---|---|---|
| ① | 正規分布 | データがどのように広がるかを理解する |
| ② | 偏差値 | σを使って個人の位置を数値化する |
| ③ | 確率と信頼区間 | データの予測や判断に応用する |
σは、単なる数学記号ではなく、「データを読む力」を支える根幹です。
σを理解すれば、統計の世界が一気に身近になり、データを見る目が変わります。
ぜひこの記事をきっかけに、次のステップとして分散や正規分布も学び、統計の基礎力を磨いていきましょう。
“シグマを制する者は、データを制す”──そんな気持ちで学びを続けていけば、数字が語る世界がぐっと面白くなります。

